Constante de Apéry

Publicado em 26 de Novembro de 2007 por Américo Tavares

pdf: ver caderno

Roger Apéry (1916-1994) surpreendeu a comunidade matemática com a sua genial demonstração de que o número real representado pela série

 \zeta(3)=\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k^3}=\displaystyle\frac{1}{1^3}+\displaystyle\frac{1}{2^3}+\displaystyle\frac{1}{3^3}+\dots

é irracional. Escolheu para a apresentar a forma de uma conferência proferida em Junho de 1978 nas “Journées Arithmétiques” de Marseille-Luminy. Utilizou um método elementar, mas que estava repleto de fórmulas complicadas e, na altura, inesperadas, sendo igualmente aplicável à série, conhecida de Euler (1707-1783),

\zeta(2)=\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k^2}=\displaystyle\frac{1}{1^2}+\displaystyle\frac{1}{2^2}+\displaystyle\frac{1}{3^2}+\dots.

    A exposição de Apéry foi acolhida com manifestações de dúvida, porventura pela estranheza provocada pela natureza das fórmulas, à primeira vista nada evidentes, e por utilizar essencialmente um método digno de Euler. Dois meses mais tarde, no Congresso Internacional de Matemáticos, H. Cohen fez uma exposição curta da demonstração, incorporando ideias suas e de D. Zagier e Apéry referiu a motivação que esteve por de trás do seu método.
    Sob a forma escrita, a demonstração de Apéry pelo próprio, data de 1979 [1] . A. van der Poorten publicou, também nesse ano, um relatório informal bastante pormenorizado e uma descrição muito viva destes acontecimentos [2]. F. Beukers apareceu, ainda em 1979, com uma elegante e mais curta demonstração da irracionalidade de \zeta(3)  [3]. Em homenagem a Apéry, a série \zeta(3) passou a ser conhecida por constante de Apéry.

     Como é sabido, os números reais podem ser classificados em números racionais, que são aqueles que podem ser expressos por fracções (ou razões) de números inteiros (por exemplo \frac{5}{2}) e os que não podem, os chamados números irracionais (por exemplo \sqrt{2}, \pi, e). Há dois tipos distintos de irracionais: os algébricos e os transcendentes. Os algébricos são zeros (ou raízes) de um polinómio de coeficientes racionais (por exemplo \sqrt{2}, visto que x=\sqrt{2} verifica a equação x^2-2=0), os transcendentes não.
    Não se sabe se a constante de Apéry, \zeta(3), é transcendente. O mais conhecido de todos os irracionais, o \pi, é transcendente como foi demonstrado por F. Lindemann em 1882. A transcendência da base dos logaritmos naturais, e, foi provada em 1873 por C. Hermite. Quanto a \zeta(2), Euler demonstrou que era igual a \displaystyle\frac{\pi^2}{6}, logo transcendente, porque todas as potências inteiras de \pi são transcendentes.
    Euler, por analogia com a factorização de um polinómio de grau n com zeros x_1, x_2, \dots, x_{n}

P(x)=c\left(1-\left(\displaystyle\frac{x}{x_1}\right)\right)\left(1-\left(\displaystyle\frac{x}{x_2}\right)\right)\left(1-\left(\displaystyle\frac{x}{x_3}\right)\right)\cdots\left(1-\left(\displaystyle\frac{x}{x_n}\right)\right),

muito embora \text{sen} \pi x tenha uma infinidade de zeros (x=0,\pm1,\pm2,\dots), teve a intuição de aplicar este conceito a esta função -  cujo desenvolvimento em série de Taylor é

 \text{sen}\; \pi x=\displaystyle\frac{\pi}{1!} -\displaystyle\frac{\left(\pi x\right)^3}{3!}+\displaystyle\frac{\left(\pi x\right)^5}{5!}\mp\cdots

fazendo

\text{sen}\; \pi x=\pi x\left(1-\left(\displaystyle\frac{x}{1}\right)\right)\left(1+\left(\displaystyle\frac{x}{1}\right)\right)\left(1-\left(\displaystyle\frac{x}{2}\right)\right)\cdots\left(1+\left(\displaystyle\frac{x}{2}\right)\right)\cdots

=\left(1-\left(\displaystyle\frac{x^2}{1}\right)\right)\left(1+\left(\displaystyle\frac{x^2}{4}\right)\right)\left(1-\left(\displaystyle\frac{x^2}{9}\right)\right)\cdots

    O factor \pi resulta de \underset{x\rightarrow 0}{\lim }\displaystyle\frac{\text{sen}\; \pi x}{x}=\pi. Igualando os coeficientes do termo em x^3, vem

\displaystyle\frac{1}{3!}\pi^3 =\pi\left(\displaystyle\frac{1}{1}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{9}+\cdots\right) =\pi\zeta(2),

o que dá \zeta(2)=\displaystyle\frac{\pi^2}{6}. Embora não seja ainda uma verdadeira demonstração, Euler veio a efectuá-la mais tarde, depois de verificar que a mesma não era desmentida numericamente. Para \zeta(4)=\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k^4}, obteve o resultado \displaystyle\frac{\pi^4}{90} e descobriu a fórmula geral de \zeta(2n)=\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k^{2n}}, que é um múltiplo racional de \pi^{2n}, isto é, \displaystyle\frac{\zeta(2n)}{\pi^{2n}} é racional. Daqui se conclui que \zeta(2n) é transcendente.

   Quanto a \zeta(2n+1)=\displaystyle\sum_{k=1}^{\infty}\displaystyle\frac{1}{k^{2n+1}}, para n\ge 2, ainda não se conseguiu demonstrar a sua irracionalidade ou racionalidade. Mas já se sabe, por exemplo, que há uma infinidade de valores de \zeta(2n+1) que são irracionais. 

    A função zeta de Riemann é tradicionalmente designada por \zeta(s), com s complexo. A função y=\zeta(x) é definida nos reais, para x>1 pela série

\zeta(x)=\displaystyle\sum_{n=1}^{\infty}\displaystyle\dfrac{1}{n^{x}}.

\bigskip

zetagrafico

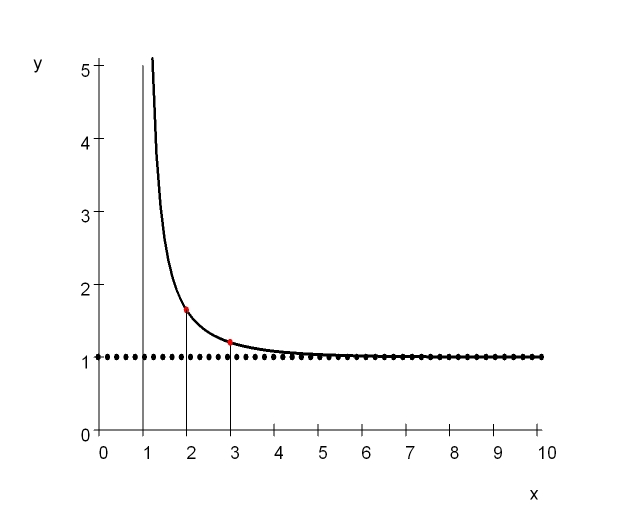
 Gráfico de \zeta(x)

   A estrutura geral da demonstração de Apéry baseia-se na construção de duas sucessões cuja razão \displaystyle\frac{u_{n}}{v_{n}} converge para \zeta(3) por valores inferiores: uma de inteiros (v_{n})_{n\ge0} e outra de racionais (u_{n})_{n\ge0}, as duas verificando a mesma relação de recorrência, mas geradas por condições iniciais distintas. A sucessão (u_{n})_{n\ge0} é tal que multiplicando u_{n} pelo termo geral duma terceira sucessão de inteiros (s_{n})_{n\ge0} se obtém o termo geral q_{n}=s_{n}u_{n} de uma sucessão de inteiros (q_{n})_{n\ge0}. A aproximação racional a \zeta(3),

 \displaystyle\frac{u_{n}}{v_{n}} =\displaystyle\frac{p_{n}}{q_{n}} (com p_{n}=s_{n}v_{n})

tem uma velocidade tal que permite concluir a irracionalidade de \zeta(3).
    Na demonstração de Beukers, o raciocínio é semelhante, com a grande diferença das fórmulas definidoras das sucessões de inteiros e de racionais, que são dadas por integrais, enquanto que nas de Apéry aparecem coeficientes binomiais. Por exemplo,

v_{n}=\displaystyle\sum_{k=0}^{k=n}\dbinom{n}{k}^2\dbinom{n+k}{k}^2

 são os chamados números de Apéry (associados a \zeta(3) ).
       
    Numericamente, tem-se

\zeta(3)=1,202056903\dots,

    e

\zeta(2)=\displaystyle\frac{\pi^2}{6}=1,644934\cdots.

Referências

[1] R. Apéry, Irrationalité de ζ(2) et ζ(3), Astérisque 61 1979, 11-13.

[2] A. van der Poorten, A Proof that Euler Missed…, Apéry’s proof of the irrationality of ζ(3). An informal report, Math. Intelligencer 1, nº 4, 1978/79, pp. 195-203. (aqui e aqui)

[3] F. Beukers, A note on the irrationality of ζ(2) and ζ(3), Bull. Lond. Math. Soc. 11, nº 33, 1978, pp. 268-272. (aqui)

Ver também http://wain.mi.ras.ru/zw/

Sobre Américo Tavares

eng. electrotécnico reformado / retired electrical engineer
Esta entrada foi publicada em Caderno, Divulgação, Matemática, Teoria dos Números com as etiquetas , , , . ligação permanente.

3 respostas a Constante de Apéry

  1. Ítalo diz:
    8 de Maio de 2014 às 14:55

    Poste muito bom, professor!
    Abraço.

    Responder
    • Américo Tavares diz:
      8 de Maio de 2014 às 23:10

      Caro Ítalo

      Obrigado por este seu comentário e ou outros dois que fez hoje. Já agora, se vir na página “Acerca de”, ficará a saber que sou um eng. reformado que gosta de Matemática.

  2. Ítalo Toffolo diz:
    13 de Junho de 2014 às 09:51

    Eu tinha visto! Nós, brasileiros, temos o costume de chamar todos que se dedicam a postar conteúdos didáticos de professores, mesmo que não sejam formados na área.
    Sou um estudante de engenharia elétrica. Amo matemática! Resido em Salvador, Bahia, Brasil.
    Abraço, sr. eng.!

    Responder

Deixe um comentário

Este site utiliza o Akismet para reduzir spam. Fica a saber como são processados os dados dos comentários.