Séries de Fourier 2 – Relação de Parseval

Publicado em 7 de Junho de 2008 por Américo Tavares

pdf: ver caderno

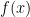Na entrada anterior abordei o caso dos sistemas completos, em que \sum c_{n}\phi_{n}(x) converge em média para f(x). A convergência em média não implica  convergência em todos os pontos.

Se considerarmos duas funções, f_{1}(x) e f_{2}(x), que diferem apenas num número finito de pontos e calcularmos os coeficientes

c_n=\dfrac{\left ( f_i\cdot \overline{\phi }_{n}\right)}{\left\vert \left\vert \phi _{n}\right\vert \right\vert ^{2}}\qquad (i=1,2)

obtemos o mesmo valor, visto que

\displaystyle\int_{a}^{b}f_i(x)\overline{\phi_{n}(x)}\; dx=(f_i\cdot\overline{\phi_{n}(x)})\qquad (i=1,2)

tem o mesmo valor para as duas funçoes, o que leva a que ambas sejam representadas pela mesma série de Fourier, ou seja, a série de Fourier pode não convergir para o valor da função num conjunto finito de pontos.

Para os sistemas completos é possível deduzir a seguinte relação:

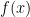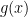Dadas duas funções f(x) e g(x) representadas pelas séries

f(x)=\displaystyle\sum c_{n}\phi_{n}(x)

g(x)=\displaystyle\sum d_{n}\phi_{n}(x)

pode demonstrar-se

  1. \displaystyle\int_{a}^{b}f(x)\overline{g}_{n}(x)\; dx=\displaystyle\sum c_{n}\overline{d}_{n}||\phi_n||^2
  2. \displaystyle\int_{a}^{b}|f(x)|^2\; dx=\displaystyle\sum |c_{n}|^2||\phi_n||^2, fazendo em 1. g(x)=f(x).

À relação 1. costuma chamar-se relação de Parseval na forma geral; à seguinte, chamar-se-á relação de Parseval na forma particular. Se soubermos de antemão que um determinado sistema de funções é completo, podemos determinar a soma de certas séries de interesse prático, à custa da relação de Parseval. 
\bigskip
Exemplo 2: O sistema de funções \sin nx (n=1,2,\dots) é ortogonal no intervalo \lbrack 0,\pi\rbrack . Determine os coeficientes de Fourier da série
f(x)=1=\displaystyle\sum_{n=1}^{\infty}c_{n}\sin nx \qquad\qquad (0\le x\le\pi)

e verifique que aquele sistema é completo em relação a esta função.
\bigskip

Começo por calcular as quantidades:
||\phi_n||^2=||\sin nx||^2=\displaystyle\int_{0}^{\pi}\sin^{2}nx\; dx=\displaystyle\int_{0}^{\pi}\dfrac{1}{2}(1-\cos 2nx)\; dx =\dfrac{\pi}{2}-\dfrac{1}{2}(\sin 2nx-\sin 0)=\dfrac{\pi}{2}

\bigskip
(f\cdot\overline{\phi}_n)=\displaystyle\int_{0}^{\pi}\sin nx\; dx=-\dfrac{1}{n}(\cos n\pi -\cos 0)=\dfrac{2}{n}, para n ímpar e
(f\cdot\overline{\phi}_n)=\displaystyle\int_{0}^{\pi}\sin nx\; dx=-\dfrac{1}{n}(\cos n\pi -\cos 0)=0, para n par
\bigskip
Deste modo

c_n=\dfrac{\left ( f\cdot \overline{\phi }_{n}\right)}{\left\vert \left\vert \phi _{n}\right\vert \right\vert ^{2}}=0, se n é par e

c_n=\dfrac{\left ( f\cdot \overline{\phi }_{n}\right)}{\left\vert \left\vert \phi _{n}\right\vert \right\vert ^{2}}=\dfrac{4}{n\pi}, se n é ímpar.

Podemos agora verificar se a igualdade

\displaystyle\int_{a}^{b}|f(x)|^2\; dx=\displaystyle\sum_{n=1}^{\infty}|c_{n}|^2||\phi_n||^2

é satisfeita: temos
\displaystyle\int_{0}^{\pi}|f(x)|^2\; dx=\pi
\displaystyle\sum_{1,3,\dots}^{\infty}|c_{n}|^2||\phi_n||^2=\dfrac{16}{\pi^2}\dfrac{\pi}{2}\displaystyle\sum_{1,3,\dots}^{\infty}\dfrac{1}{n^2}=\dfrac{8}{\pi}\dfrac{\pi^2}{8}=\pi=\displaystyle\int_{0}^{\pi}|f(x)|^2\; dx
o que significa que o sistema \sin nx é completo em relação à função f(x)=1, x\in\lbrack 0,\pi\rbrack . \blacktriangleleft
\bigskip
NOTA: Utilizei a soma da série \displaystyle\sum_{1,3,\dots}^{\infty}\dfrac{1}{n^2}=\dfrac{\pi^2}{8}. Um dos métodos é descrito no livro de Taylor (ver consultas), p. 717:
Desenvolve-se em série trigonométrica de Fourier, que será vista posteriormente,  a função f(x)=\dfrac{\pi^2}{4}, x\in\lbrack -\pi,\pi\rbrack , chegando-se a 
\dfrac{\pi^2}{12}=\dfrac{1}{1^2}-\dfrac{1}{2^2}+\dfrac{1}{3^2}-\dfrac{1}{4^2}\pm\cdots,
\bigskip
\dfrac{\pi^2}{6}=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\cdots.
Somando-as, obtém-se
\dfrac{\pi^2}{8}=\dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\cdots.
\bigskip
Nota: nesta entrada também escrevi sobre esta relação.

Actualização de 18-11-2008: ligeiras correcções nas fórmulas e no texto e inclusão da versão em pdf.

Sobre Américo Tavares

eng. electrotécnico reformado / retired electrical engineer
Esta entrada foi publicada em Análise de Fourier, Análise Matemática, Caderno, Cálculo, Matemática, Séries, Teorema / Teoria com as etiquetas , . ligação permanente.

Deixe um comentário

Este site utiliza o Akismet para reduzir spam. Fica a saber como são processados os dados dos comentários.