A forma canónica da equação do 4.º grau ou quártica é:
com
À semelhança do que foi feito para a equação cúbica, faz-se a substituição :
Ordenando pelas potências decrescentes de fica:
Se dividirmos por e anularmos o termo em
, para o que devemos fazer
obtemos a equação reduzida
sendo os seus coeficientes dados por
e
Um dos métodos de resolução é o que usa uma equação cúbica auxiliar e que descrevo de seguida. O outro — que nem sempre funciona — é a factorização do 1.º membro da equação em dois factores do segundo grau.
Se somarmos e subtrairmos ao primeiro membro de
, por razões que se tornarão evidentes mais abaixo, obtemos a equação equivalente:
Desenvolvemos a parcela em factores lineares:
em que e
são as soluções da equação do 2.º grau
Assim se o discriminante
for nulo, o que significa que verifica a equação cúbica:
então
e
pelo que a equação se transforma em
Factorizando agora o primeiro membro ficamos com a equação:
cujas soluções são imediatas: as que anulam o primeiro factor verificam a equação do 2.º grau em :
e as que anulam o segundo verificam a equação do segundo grau em
As soluções da equação reduzida são as duas de
:
e as duas de :
em que é uma solução da equação cúbica auxiliar
que se repete
As soluções da equação do 4.º grau inicial são pois:
Exemplo: Resolva
Vemos que
,
,
,
e
Calculamos os coeficientes da equação reduzida
obtida pela substituição :
e
A equação cúbica auxiliar é, pois:
Determinação de uma solução real da equação cúbica: os seus coeficientes são
Nota: estas letras ,
,
, e
, embora iguais às utilizadas acima para designar os coeficientes da equação quártica, aqui designam os coeficientes da cúbica.
Pondo
a equação cúbica transforma-se em
visto que
e
Uma solução da equação cúbica é:
As soluções da equação são então:
Edição de 24.06.2013: corrigida gralha na nota. Corrigido ainda nas fórmulas de
do exemplo. Ver comentários de hoje do leitor Pedro.
—
Referências
WolframMathWorld, Quartic Equation
Ask Dr. Math, What are the general solutions to cubic and quartic polynomial equations?










Mais uma vez, com paciência, dedicação e destreza, você apresentou o assunto sobre as equações quárticas de forma brilhante. Parabéns!
Neste link, eu apresento um caso particular da equação quártica que serve como assunto motivador para o caso geral.
http://fatosmatematicos.blogspot.com/2009/06/um-caso-particular-da-equacao-quartica.html
muito legal, gostei, apresentação clara
Texto relevante, com explicação muito clara e abordada de maneira singular. Parabéns pelo conteúdo nobre publicado neste website.
Obrigado!
não entendir nada
Boa tarde! Gostei muito do post de resolução de equações do 4º grau, mas fiquei com uma dúvida. As expressões para o cálculo das raízes x1, x2, x3 e x4 somente são aplicáveis se s1 for um número real?
Desde já agradeço,
JS.
Obrigado!
Qualquer solução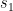 real ou complexa serve, mas os cálculos são muito mais fáceis se escolhermos uma solução real. E essa escolha é sempre possível porque uma equação cúbica com coeficientes reais tem uma ou três soluções reais.
real ou complexa serve, mas os cálculos são muito mais fáceis se escolhermos uma solução real. E essa escolha é sempre possível porque uma equação cúbica com coeficientes reais tem uma ou três soluções reais.
A resposta veio mais rápido do que eu imaginava. Muito obrigado!
Agora, perdoa-me se eu estiver falando algum absurdo. Se posso escolher qualquer uma das soluções da equação cúbica auxiliar para econtrar as solução da equação quártica, não haveria três conjuntos de soluções diferentes para a equação quártica?
Desde já agradeço,
JS.
Caro JS.
Fiz alguns testes com raízes da equação de 4º grau com outras raízes de 3º grau, em que x’ trocando o resultado chegava em x”’; então penso que não resultem em 3 conjuntos, talvez em casos específicos.
Pedro
Agora estou considerando as possibilidades que levem ao resultado de apenas um conjunto solução. Quando se foi considerado que , os valores de s que satisfazem o valor de y são os que tornam a equivalência a zero e resultem na equação original de mesma forma. E testando cheguei ao mesmo resultado.
, os valores de s que satisfazem o valor de y são os que tornam a equivalência a zero e resultem na equação original de mesma forma. E testando cheguei ao mesmo resultado.
Pedro.
A sua questão é bastante pertinente e não sei dar-lhe uma resposta cabal. É possível que no âmbito da Teoria de Galois a haja, mas não tenho conhecimentos para o afirmar. O meu primeiro comentário resultou de ter visto na versão inglesa da Wikipedia a confirmação de que se poderia escolher qualquer das soluções da cúbica auxiliar (nota: não verifiquei a equivalência da equação cúbica dessa entrada — “nested depressed cubic” — com a que apresento acima). A este respeito o forum Ask Dr. Math refere o mesmo. Quanto a mim, em termos numéricos, sempre escolhi a solução real da cúbica, como no exemplo que apresento.
A minha interpretação é que como as três soluções de uma equação cúbica reduzida se podem exprimir numa única fórmula (a de Cardano), com duas parcelas que estão ligadas por uma condição envolvendo os coeficientes, tudo se conjugará para que essa condição mais a inerente à da equação quártica propriamente dita, acabe por reduzir o número de soluções independentes da quártica a quatro, qualquer que seja a escolha feita. Mas não conheço uma demonstração do que estou a afirmar. Apenas tenho uma coisa por certa: o número de soluções da quártica é quatro.
Não consegui chegar em x3=0,70062; cheguei em 0,700598337 que é aproximadamente 0,70059 ou 0,70060
0,70060 ≠ 0,70062
o mesmo em x4= -0,35095; achei -0,350916832; que é aproximadamente -0,35091 ou -0,35092
-0,35092 ≠ -0,35095
Obtive no Quartic/Cubic/Quadratic Equation Calculator (http://www.freewebs.com/brianjs/ultimateequationsolver.htm ) as seguintes raízes (numeradas de forma diferente da do post):
Os valores do post foram calculados no SWP, que tem uma menor precisão. Não os cheguei a calcular com uma calculadora científica. E o erro na aproximação da raíz da cúbica propaga-se às da quártica.
Conclusão: os seus valores são mais precisos do que os que calculei.
PS. O mesmo calculador dá como solução real da equação cúbica (na minha notação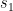 )
)  .
.
Novamente seu post foi esclarecedor e objetivo, com ele consegui fazer a calculadora de equações de 4º grau, obrigado, possui alguma fórmula resolvente para equações de 5º grau em geral?
Não tenho, nem há do tipo das do 1.º, 2.º, 3.º e 4.º grau! Foi demonstrado pelo matemático norueguês Niels Henrik Abel que as soluções da equação geral do 5.º grau (ou quíntica)
não se podem exprimir em um número finito de operações algébricas: soma, subtracção, multiplicação, divisão, potênciação e radiciação, embora haja casos particulares da quíntica que são solúveis. É um resultado muito importante do séc. XIX. Pode começar por ver na Wikipédia o Teorema de Abel-Ruffini
http://pt.wikipedia.org/wiki/Teorema_de_Abel-Ruffini
ou a versão inglesa Abel–Ruffini theorem que é muito mais desenvolvida
http://en.wikipedia.org/wiki/Abel%E2%80%93Ruffini_theorem.
Sendo assim as soluções da equação quíntica ou outras de ordem superior são calculadas por métodos numéricos. Claro que os casos particulares que se saiba terem solução podem ser calculados sem ser só por esses métodos numéricos.
Veja na Wikipédia a Equação do quinto grau
http://pt.wikipedia.org/wiki/Equa%C3%A7%C3%A3o_do_quinto_grau
e, em inglês,
Quintic function http://en.wikipedia.org/wiki/Quintic_function.
Suponha que tem uma equação quíntica
com coeficientes numéricos. Como tem obrigatoriamente de ter pelo menos uma solução real, pode procurá-la por um método numérico, por exemplo de Newton ou da secante. Se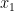 for uma solução encontrada, então divide
for uma solução encontrada, então divide
por
obtendo uma equação quádrupla, que já sabe como resolver.
No exemplo 1: “Nota: estas letras a, b, c e d, embora iguais às utilizadas acima para designar os coeficientes da equação quadrática, aqui designam os coeficientes da cúbica.”
Não deveria ser: Nota: estas letras a, b, c, e d, embora iguais às utilizadas acima para designar os coeficientes da equação quártica, aqui designam os coeficientes da cúbica.
Obrigado! Corrigido.
P.S. Vejo que está a ler com muita atenção todo o post, como terá lido também com igual atenção o das equações cúbicas!
Também reparei que nos exemplos da equação quártica está com s1 e s para representar a solução auxiliar:
em que deveria estar ou ou
ou 
Mais uma vez, obrigado!
Corrigi, ficando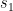 nas fórmulas de
nas fórmulas de  do exemplo.
do exemplo.
se quiser colocar também os exemplos que resulta nas raízes:
que resulta nas raízes: 

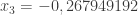
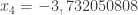
e o exemplo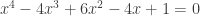
cujas soluções são imediatas por: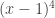 ;
;
portanto x1=x2=x3=x4=1
Ao seu primeiro exemplo
pode aplicar-se o Teorema das raízes racionais
( http://pt.wikipedia.org/wiki/Teorema_das_ra%C3%ADzes_racionais )
pelo qual, a haver raízes racionais, estas só poderão ser . Substituindo na equação vemos que apenas
. Substituindo na equação vemos que apenas 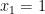 é solução. As outras três são as raízes do polinómio do 3.º grau, quociente da divisão polinomial de
é solução. As outras três são as raízes do polinómio do 3.º grau, quociente da divisão polinomial de
por
isto é as raízes da cúbica
Correcção .
.
As segundo também se pode aplicar o mesmo teorema.
Mas dividindo por (x-1), o resultado é: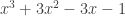 e não
e não 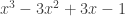
Repare
Confirmação
isso é completamente desnecessário, pois pode-se fatorar por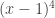 como disse no outro comentário; e a fatoração de 1 não é
como disse no outro comentário; e a fatoração de 1 não é  e sim
e sim 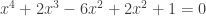
OK. Já corrigi no comentário. Obrigado.
Caro Américo Tavares, estou pensando em um modo de achar as soluções da equação quíntica a partir de uma raiz, e gostaria de lhe enviar por E-Mail.
Pedro
Aguardando resposta
favor desconsiderar meu E-Mail, resultados errados.
Caro Pedro
Gostaria de saber sobre seu trabalho com as equações de 5° e 6°. Mas confesso que sou apenas um entusiasmado jovem com matemática e que provavelmente não trará avançoes a sua pesquisa. Mesmo peço contato por e-mail.
Desde já grato.
Caro Américo Tavares, reparo que em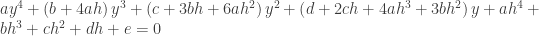 , mais precisamente na parte
, mais precisamente na parte 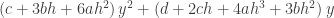 existem 2 sinais de soma.
existem 2 sinais de soma.
Pedro
Obrigado, já mudei a formatação da equação e suprimi um dos sinais.
Caro Américo Tavares,
Estou pesquisando um pouco sobre Equações de sexto grau, e tenho alguns resultados interessantes. Se acabar chegando em alguma conclusão útil estaria interessado em visualizá-los? Se sim comente e lhe enviarei um E-Mail.
Pedro
envia pra mim gostaria de ver esse seus resultados
e-mail:joao_liu@hotmail.com.br
Caro Américo Tavares
Cai nesse site por sorte e acabei achando essas suas soluções e explicações ótimas então primeiramente obrigado.
Agora em segundo eu cheguei a conclusão que todas as equações de grau P^n (P um primo) podem ter suas raízes reveladas (não falo de uma formula geral mas sim de encontrar as raízes) e por tabela todas as equações com grau de número composto (contanto que já tenha soluções para as equações de grau P de seus divisores claro) pelas relações de Goulart e queria saber se isso é possível, se já descobriram isso, e se o senhor poderia me ajudar a compreender isso
A fórmula é bacana, mas, ainda prefiro método de Newton rsrs
Mesmo assim, ainda jade se pensar no trabalho caso haja 3 soluções para s ?
Aplicando o método de viet achamos os 3 valores de s, porém, temos que testa-los, seria isso?
é horrivel aplicar essa formula cardano mds da uma dor de cabeça so vi 1 equaçao em que foi facil aplica-la e é a equaçao x³-3x-2 pq no resto.Muito ao contrario da formula de bhaskara que qualquer um mesmo com poucos conhecimentos matematicos pode resolver;.
Americo por acaso vc ja tentou desenvolver um metodo para equaçoes do 5 grau (n digo formula pq o teorema afirma q n existe) mas talves uma sequencia de passos para resolve-la?seria possivel??
existe algum metodo ou algoritimo para resolver uma equaçao do 5 grau nao digo uma formula pois nao existe
Pode calcular por métodos numéricos uma raiz real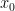 , visto que existirá pelo menos uma. A partir daqui dividir o polinómio dado por
, visto que existirá pelo menos uma. A partir daqui dividir o polinómio dado por  , obtendo assim um do 4. grau.
, obtendo assim um do 4. grau.
Ei e o que se faz quando e uma equaçao e de grau par(diz q grau impar possui uma soluçao real)
como faria para calcula-la? ( caso o teorema das raizes racionais nao me der raiz)
e esse Niels Henrik Abel esse teorema dele e realmente confiavel? sera que uma equaçao do 5 grau possua formula e eles que nao quiseram encontrar?
Se um polinómio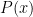 for de grau ímpar, para
for de grau ímpar, para  positivo e suficientemente grande o valor de
positivo e suficientemente grande o valor de 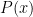 há de ser positivo. Para
há de ser positivo. Para  fortemente negativo,
fortemente negativo, 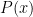 será negativo. Como
será negativo. Como 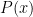 é uma função contínua há de passar pelo menos uma vez por
é uma função contínua há de passar pelo menos uma vez por 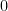 . Se
. Se 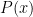 for de grau par, então, para
for de grau par, então, para  fortemente positivo ou negativo,
fortemente positivo ou negativo, 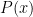 será necessariamente positivo. Por isso não se pode garantir, em geral, que tenha um zero real. Por exemplo
será necessariamente positivo. Por isso não se pode garantir, em geral, que tenha um zero real. Por exemplo  é sempre positivo. Se do teorema que refere não se deduzir que haja zeros racionais, em geral só poderá tentar aplicar métodos numéricos. Uma das soluções é
é sempre positivo. Se do teorema que refere não se deduzir que haja zeros racionais, em geral só poderá tentar aplicar métodos numéricos. Uma das soluções é 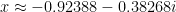 . Quanto ao teorema de Abel não há qualquer dúvida que é verdadeiro. Veja, por exemplo, a página da Wikipédia “Teorema de Abel-Ruffini” da qual cito: “a solução de uma equação de grau cinco ou superior não pode ser sempre expressa a partir dos coeficentes e usando simplesmente as operações de adição, subtração/subtracção, multiplicação, divisão e potenciação (incluindo-se nesta última a extração/extracção de raízes”.
. Quanto ao teorema de Abel não há qualquer dúvida que é verdadeiro. Veja, por exemplo, a página da Wikipédia “Teorema de Abel-Ruffini” da qual cito: “a solução de uma equação de grau cinco ou superior não pode ser sempre expressa a partir dos coeficentes e usando simplesmente as operações de adição, subtração/subtracção, multiplicação, divisão e potenciação (incluindo-se nesta última a extração/extracção de raízes”.