Tem cinco moedas iguais, cada uma a tocar nas duas adjacentes. No espaço que fica no meio coloca uma moeda tangente às cinco.
Qual é a área total entre as moedas em função do diâmetro 
Five equal coins are placed in such a way that each of them is tangent to the two adjacents ones. Another coin tangent to those five is put in the centre.
Find the total area between the coins as a function of the diameter
Figura auxiliar / Auxiliar figure
Neste caso o $0.05 não é bem tangente aos €0.50.
In this case the $0.05 coin is not quite tangent to the five €0.50 coins.
Imagine que as moedas eram círculos ideais, tangentes 3 a 3, excepto o central a 5.
Suppose all the coins are ideal circles arranged so that each is tangent to 3 , except the central one which is tangent to the other 5.
P.S. English text edited.
Problemas e Teoremas 
Resolução de RSCS de 27.03.10, em
publicada em comentário a
http://simplesmenteporquesim.wordpress.com/2010/03/26/quando-mais-nada-ocorre/ .
Substituindo os resultados parciais na área final indicada na resolução, obtive, em função de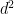
, para a área pedida:
ou seja
[31.03.10: Corrigi autor da solução]