![]() ver/see Problema do mês Problem of the month
ver/see Problema do mês Problem of the month
Enunciado do Problema
Seja
o maior inteiro positivo tal que
Determine, justificando, um majorante de
- Nota: não se permite a utilização de calculadoras ou computadores.
- Sairá vencedora a melhor estimativa justificada.
- Afirmação não demonstrada: 10 é um majorante de
. Encontre um mais pequeno.
- O prazo limite para apresentar resoluções é 19.07.2009. acltavares@sapo.pt
Problem Statement
Let
be the greatest positive integer such that
Find with proof an upper bound for
- Remark: the use of calculators or computers is not allowed.
- The best justified estimate will win.
- Claim: 10 is an upper bound for
. Find a smaller one.
- The deadline for submitting solutions is July 19, 2009. acltavares@sapo.pt










Bonjour Américo,
J’ai essayé de donner une réponse à la question :
http://allken-bernard.org/pierre/weblog/?p=744#comment-1025
A bientôt.
[On sait que De
De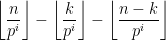
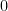 ou
ou 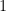 (on a toujours
(on a toujours  qui vaut
qui vaut 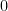 ou
ou 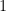 ).
).
plus, chaque terme
vaut
Si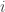 est assez grand, il est clair que
est assez grand, il est clair que  . Précisément, puisque
. Précisément, puisque 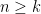 , il
, il , c’est-à-dire
, c’est-à-dire  pour que
pour que 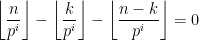 . On a donc:
. On a donc: 
suffit que
Donc . Et
. Et  c’est mieux que
c’est mieux que 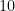 :) ] Added/Acrescentado A Tavares
:) ] Added/Acrescentado A Tavares
Bonjour et merci PB,
J’ai transcrit votre réponse.
A bientôt.
C’est moi qui vous remercie :-)
Mais est-on certain que 5 est la bonne réponse ?
Américo Tavares
(edit)
PB
Yes, but I am not able to prove it theoretically.
The proof I know is just a short version of yours.
Let us see if someone can prove it.
5 deve ser a melhor resposta.
Pingback: Walking Randomly » New math problem of the month series
Em 13.06.09 divulguei este problema nos Gaussianos.
On July 13, 2009 I posted this Problem in Gaussianos.