A curva de perseguição ou do cão (em inglês pursuit curve ) é uma curva clássica que foi estudada, entre outros, por Pierre Bouguer, em 1732. Consiste na trajectória descrita por um ponto chamado perseguidor que se move em cada instante em direcção a outro, o perseguido. A curva descrita por este é conhecida por curva de fuga, sendo uma recta, no caso mais simples, como é o do problema deste post. O móvel perseguidor e o perseguido podem representar, por exemplo, um cão e um gato, um homem e um porco, como neste puzzle antigo de Sam Loyd’s, dois aviões, navios, etc. Pode ver-se uma demonstração animada em Hundenkurven.
Na questão Cat Dog problem using integration de pokrate, no MSE, é enunciado o seguinte problema que parece ter aparecido numa competição (das Olimpíadas da Física, segundo esta questão de Physics Forums), mas não consegui confirmar, e que passo a traduzir:
« Um gato sentado num campo vê de repente um cão. Para se salvar o gato foge em linha recta à velocidade
. O cão começa logo a correr a uma velocidade constante
para caçar o gato. No instante inicial a distância que os separa é
e
é perpendicular a
. Se o cão mudar constantemente de direcção, de modo a que esteja sempre a apontar para o gato, determinar o tempo que demora a apanhá-lo, em termos de
e
. »
Eis uma tradução da solução que apresentei:
Admita-se que: (a) o cão parte do ponto e o gato da origem
; (b) o gato move-se no sentido positivo ao longo do eixo dos
, e o cão descreve uma curva de perseguição
no plano
. Seja
a equação de
.
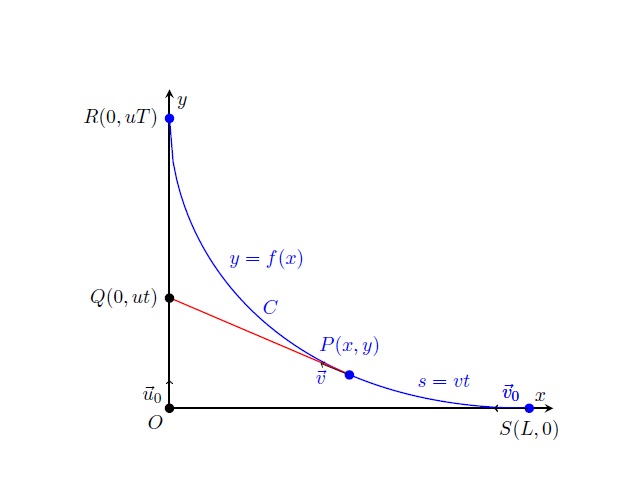
1. No instante a tangente a
no ponto
passa pelo ponto
, o que significa que a derivada
é
Resolvendo em ordem a obtemos
2. Seja a distância percorrida pelo cão de
a
, ou seja o comprimento do arco
medido ao longo de
. Como a fórmula do comprimento de um arco é o integral
e , tem-se
Igualando as duas expressões de será pois
3. Diferenciando ambos os membros e simplificando vem
obtendo-se a seguinte equação diferencial
4. Fazemos agora e resolvemos em ordem a
, aplicando o método de separação de variáveis, pelo que teremos
Logo
As condições iniciais determinam o valor da
constante de integração
Consequentemente
Resolvendo em ordem a e exprimindo em termos de funções exponenciais, atendendo à definição de
, obtemos
Esta segunda equação diferencial é facilmente integrável
Determinamos através das condições iniciais
Chegamos assim à equação da trajectória:
5. Para obter o tempo que o cão demora a apanhar o gato, basta fazer
nesta equação e atender a que que o gato percorre a distância
:
donde
* * *
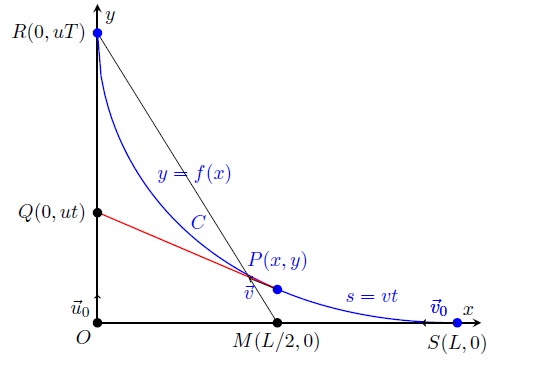
Nota 1: pode verificar-se facilmente que o comprimento da curva é igual à soma dos comprimentos dos segmentos de recta
e
. O ponto
está situado a meio da distância do ponto
à origem
.
Nota 2: se o perseguidor nunca apanha o perseguido, como pode ver nas animações de Hundenkurven.
Nota 3: os gráficos foram criados como tikzpictures, em . O código foi adaptado desta resposta de percusse a esta minha questão no TEX (tex.stackexchange).
—
Referências:
Michael Lloyd, Pursuit Curves
Pursuit curve, Wikipedia (inglês)
Radiodrome, Wikipedia (alemão)
Pursuit curve, MathWorld
Helmut Knaust, The Curve of Pursuit
Carl E Mungan, A classic chase problem solved from a physics perspective
Dennis G. Zill, Michael R. Cullen, Michael R. Cullen, Differential Equations with Boundary-Value Problems, Exercise 5.17, p. 214










Tomei conhecimento deste problema como curiosidade nas olimpíadas da física portuguesas (já há 3/4 anos, ainda frequentava o ensino secundário).
Realmente a resolução que apresenta é detalhada e completa, como os matemáticos gostam, mas o desafio (nas olimpiadas) era o problema ser feito por alunos do 12º ano, e sem equações diferenciais obviamente. Claro que o rigor matematico não era a prioridade, e era engraçado ver as várias sugestões de resolução.
É engraçado anos depois ler este post e ver a resolução completa, obrigado.
Obrigado, eu, pela informação que aqui deixa. Gostaria de ver algumas abordagens mais elementares, quase de certeza muito mais engenhosas que esta.
Existirá algum link para o enunciado original e alguma solução?
Uma pequena nota: sou um eng. reformado com interesse na Matemática, mas dela só tenho conhecimentos gerais e um ou outro mais específico de nível um pouco mais elevado.
Não entendi o passo em que “…que a derivada y’=f'(x)=dy/dx é y’=(y-ut)/x” Qual é o raciocínio dessa última afirmação?
Obrigado!
A derivada é igual ao declive da recta tangente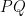 .
.
Valeu Américo… Eu tinha me confundido com a distância x, não observei o ponto P. Parabéns pelo blog!
Obrigado!
Reblogged this on Problemas e Teoremas and commented:
Republico temporariamente este problema.
Show, usarei em minhas aulas!