Em resposta a uma questão de George Edison, no MSE, apresentei as seguintes duas demonstrações de
Demonstração 1. (Dias Agudo, Cândido da Silva, Matemáticas Gerais III, Exercício 2.5.1). Seja . Considere-se
e some-se
para
:
O termo no primeiro membro da primeira soma cancela o termo
no segundo membro da segunda,
, o
,
, o
, …, o
cancela
. Assim
e
porque
.
Demonstração 2. (Balakrishnan, Combinatorics, Schaum’s Outline of Combinatorics, Exercício 1.42 ). De
obtem-se










Na verdade o primeiro método apresentado pode ser facilmente generalizado para permitir o cálculo de
 iterativamente, ou seja, em função das somas
iterativamente, ou seja, em função das somas
 .
.
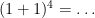

Como ilustração, poderá partir de
para obter a curiosa igualdade
Resta-me seguir o método que indica, que agradeço. Começando pelo desenvolvimento binomial
e somando membro a membro as identidades seguintes
identidades seguintes
ficamos com
Utilizando o valor da soma
e o da soma calculada acima
obtemos a equação
que resolvida em ordem a nos dá, de facto,
nos dá, de facto,
O problema das somas das potências foi tratado por Faulhaber até à 17ª e por Bernoulli na sua famosa obra Ars Conjectandi: daí os coeficientes receberem o nome de números de Bernoulli.
potências foi tratado por Faulhaber até à 17ª e por Bernoulli na sua famosa obra Ars Conjectandi: daí os coeficientes receberem o nome de números de Bernoulli. -ésima potência por
-ésima potência por  como no artigo. Como
como no artigo. Como 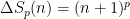 vemos que
vemos que  constitui um polinómio de grau
constitui um polinómio de grau  . Além disso, temos
. Além disso, temos 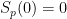 vindo, portanto,
vindo, portanto,
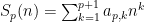

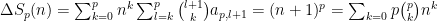
 equações, com
equações, com  ,
,

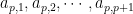 . Por exemplo, para
. Por exemplo, para  temos
temos

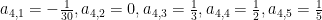
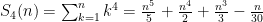
 basta observar que as colunas correspondem às linhas do triângulo de Pascal onde é ignorada a última entrada. Os termos independentes correspondem à linha
basta observar que as colunas correspondem às linhas do triângulo de Pascal onde é ignorada a última entrada. Os termos independentes correspondem à linha  completa do triângulo.
completa do triângulo.
Vou aqui apresentar o raciocínio que segui há já muito tempo para obter várias somas do género antes de as ter encontrado na literatura técnica.
Designo a soma da
Ora, daqui vem
Deste modo,
Se compararmos os coeficientes com a mesma potência temos o conjunto de
Este sistema pode ser escrito facilmente na forma matricial para os coeficientes
A solução deste sistema escreve-se como
Temos, portanto,
Para construir a matriz para outros valores de
Inteligente e esclarecedor raciocínio o seu que teve a amabilidade de aqui nos explicar.
Aproveito para indicar aos leitores que as somas se podem determinar recursivamente pela fórmula
se podem determinar recursivamente pela fórmula
Bom Ano Novo!
Essas demonstrações de séries envolvendo a soma de números inteiros são incríveis as quais de certa forma estava esquecido de algumas passagens, principalmente para somar números inteiros ao quadrado, e nem pensava na generalização, mas mesmo assim não entendi o processo utilizando a combinatória. Parabéns prof. Américo Tavares
Pingback: Coeficiente de correlação de postos de Spearman | bloqm
Gostei, apesar de n entender tudo, finalmente achei uma demonstração para isso sem ser por indução kkkk
Pingback: How to compute this sum – Math Solution